Please write or type up your solutions, and hand in a paper copy before class on Monday.
Introduction
In class, we have been discussing how Graph structures might can be used to represent relationships between groups of objects. For this assignment, you will be writing a program that allows you to play the "Kevin Bacon Game". A person's "Bacon Number" is computed based on the number of movies of separation between that person and the actor Kevin Bacon. For example, if you are Kevin Bacon, then your Bacon Number is 0. If you were in a movie with Kevin Bacon, your number would be 1. If you weren't in a movie with Kevin Bacon, but were in a movie with someone who was, your Bacon Number would be 2. In short, your Bacon Number is one greater than the smallest Bacon Number of any of your co-stars.
Note that this is a take off of Erdos numbers (mine's 3), and the two can be combined to form the more elusive Erdos-Bacon number.
For fun and some additional background, you can try out the Oracle of Bacon at the University of Virginia.
Practice with graphs
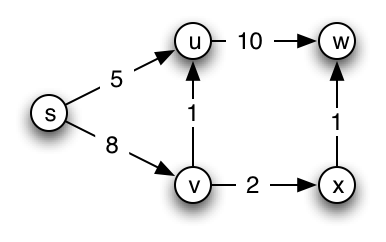
In class we developed Dijkstra's algorithm for finding the shortest paths from a Start node to every other node in weighted graphs with non-negative weights. In that algorithm we stored a vertex, its tentative distance from the Start node, and its predecessor in a priority queue. The comparator for this queue considers only the distance field. The queue starts with the Start node at distance 0, with null predecessor. Until the priority queue is empty we do the following:
- Remove the smallest node (the one with the smallest distance) from the queue. Call this node X. If X is already marked as "done", ignore it.
- If X is not yet marked, mark it now as done. For each edge from X to some other node Y, if Y is not marked as done add it to the priority queue with distance equal to the distance to X plus the weight of the edge from X to Y and with predecessor X..
-
Run Dijkstra's algorithm on the following graph. At each step keep track of the members of the priority queue, the distance to each node, and the predecessor of each node.
Kevin Bacon Game
CSLAM Studios (Computer Science Lab Assignment Movies) has a small library of movies they have released. These include:
- Best Friends Forever (BFF) featuring:
- Alice
- Bob
- Carol
- Best Friends Forever 2: The Refriendanatoring (BFF2) featuring:
- Alice
- Carol
- Dave
- Student Art Project (SAP) featuring:
- Carol
- Dave
- Eve
- My Other Movie (MOM) featuring:
- Dave
- Eve
-
Draw a graph representing the relationships between movies and actrons.
You may use initials to represent the various movies and performers.
There should be an edge with weight 0 from each actor to each movie
featuring that actor, and an edge with weight 1 from each movie to each
actor in that movie.
"Best Friends Forever" (BFF) featuring: Alice, Bob, Carol; "Best Friends Forever 2: The refriendanatoring" (BFF2) featuring: Alice, Carol, Dave; "Student Art Project" (SAP) featuring: Carol, Dave, Eve; "My Other Movie" (MOM) featuring: Dave, Eve.
- Run Dijkstra's algorithm on your graph to find the distance and best path from Bob to each other actor.

Last Modified: April 25, 2015 - Benjamin A. Kuperman
